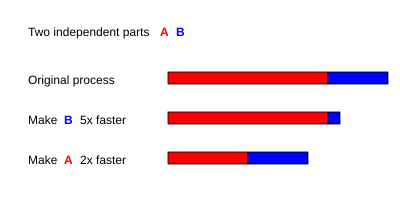
Në mënyrë optimale, rritja e shpejtësisë nga paralelizmi do të jetë lineare, dyfishon numrin e elementeve të përpunimit duke përgjysmuar kohën e ekzekutimit, dhe e dyfishon për herë të dytë përsëri, përgjysmon kohën e ekzekutimit. Megjithatë, shumë pak algoritme paralele arrijnë shpejtësin optimale. Shumica prej tyre kanë një rritje lineare të shpejtësisë për një numër të vogël të elementeve të përpunimit, të cilat sheshohen në një vlerë të vazhdueshme për një numër të madh të elementeve të përpunimit.
Potenciali i rritjes së shpejtësisë së një algoritmi në një platformë kompjuterike paralele është dhënë me ligjin e Amdahl, formuluar fillimisht nga Gene Amdahl në vitet 1960 [10]. Ky ligj thekson se një pjesë e vogël e programit, i cili nuk mund të paralelizohet do ta kufizojnë shpejtësin e përgjithshme në dispozicion nga paralelizmi. Madhësitë matematikore ose problemet inxhinierike zakonisht përbëhen nga disa pjesë të paralelizuara dhe disa pjesë jo-paralelizuara (sekuenciale). Kjo marrëdhënie jepet nga ekuacioni:
ku S është shpejtësia e programit (si një faktor i ekzekutimit sekuencial), si dhe P është pjesë që është paralelizuar. Nëse pjesa e vijues e një programi është 10% e kohës së ekzekutimit, ne mund të marrim jo më shumë se 10× herë rritje të shpejtësisë, pa marrë parasysh sa procesorë janë shtuar. Kjo e vendos një kufizim lartë në dobi të më shumë pjesëve ë ekzekutuara njëkohësisht. Kur një detyrë nuk mund të ndahet për shkak të kufizimeve sekenciale, aplikimi i më shumë përpjekjeve nuk ka efekt në program. "Sjellja e fëmijës merr nëntë muaj, pa marrë parasysh sa shumë gra janë caktuar [11].
Ligji i Gustafson është një ligj tjetër në inxhinierin kompjuterike, i lidhur ngushtë me ligjin e Amdahl. Ai mund të formulohet si:
ku P është numri i procesorëve, S është shpejtësia, dhe α - pjesët jo të paralelizuara të procesit [12]. Ligji Amdahl e merr një madhësi të caktuar të problemit dhe kjo madhësi e seksionin sekuencial është e pavarur nga numri i procesorëve, ndërsa ligji i Gustafson nuk ka bërë këto supozime.